Es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponencial de la base del logaritmo.
EJEMPLO:
PARTES DE LOGARITMO
¿COMO REPRESENTAR UN LOGARITMO?
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
| Logaritmo | ||
|---|---|---|
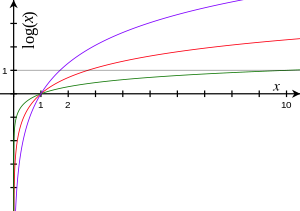 Gráfica de Logaritmo | ||
| Definición |   | |
| Tipo | Función real | |
| Descubridor(es) | John Napier (1614) | |
| Dominio | 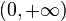 | |
| Codominio |  | |
| Imagen |  | |
| Propiedades | Biyectiva Cóncava Estrictamente creciente Trascendente | |
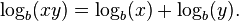
No hay comentarios:
Publicar un comentario