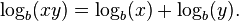lunes, 2 de febrero de 2015
CLASIFICACIÓN DE LOGARITMOS
LOGARITMO DECIMAL
Logaritmos decimales Son los de base 10, son los más usados y por este motivo no suele escribirse la base cuando se utilizan.
log 10 = log 101 =1
log 100 = log 102 =2
log 1000 = log 103 = 3
log 10000 = log 104 = 4 , …etc
Observa que entonces el log de un número de 2 cifras, comprendido entre 10 y 100, es 1,... ; el log de los números de 3 cifras será 2,... ; etc.
Por otra parte:
log 0,1 = log 10-1 = -1
log 0,01 = log 10-2 = -2
log 0,001 = log 10-3 = -3, …etc
Entonces el log de un número comprendido entre 0,01 y 0,1 será -1,...; el de uno comprendido entre 0,001 y 0,01 será -2,..., etc.
LOGARITMO NATURAL O NEPERIANO
Los logaritmos naturales o logaritmos neperianos son los que tienen base e. Se representan por ln (x) o L(x).
Los logaritmos neperianios deben su nombre a su descubridor John Neper y fueron los primeros en ser utilizados.
El logaritmo neperiano de x (ln x) es la potencia a la que se debe elevar e para obtener x.
 Cambio de base : Para realizar el cambio de base se utiliza la siguiente formula :
Cambio de base : Para realizar el cambio de base se utiliza la siguiente formula :
Logaritmos decimales Son los de base 10, son los más usados y por este motivo no suele escribirse la base cuando se utilizan.
log 10 = log 101 =1
log 100 = log 102 =2
log 1000 = log 103 = 3
log 10000 = log 104 = 4 , …etc
Observa que entonces el log de un número de 2 cifras, comprendido entre 10 y 100, es 1,... ; el log de los números de 3 cifras será 2,... ; etc.
Por otra parte:
log 0,1 = log 10-1 = -1
log 0,01 = log 10-2 = -2
log 0,001 = log 10-3 = -3, …etc
Entonces el log de un número comprendido entre 0,01 y 0,1 será -1,...; el de uno comprendido entre 0,001 y 0,01 será -2,..., etc.
LOGARITMO NATURAL O NEPERIANO
Los logaritmos naturales o logaritmos neperianos son los que tienen base e. Se representan por ln (x) o L(x).
Los logaritmos neperianios deben su nombre a su descubridor John Neper y fueron los primeros en ser utilizados.
El logaritmo neperiano de x (ln x) es la potencia a la que se debe elevar e para obtener x.
ln 1 = 0 e0 = 1

PROPIEDADES DE LOGARITMO
PROPIEDADES DE LOS LOGARITMOS
- Dos números distintos tienen logaritmos distintos.
Si 
- El logaritmo de la base es 1
- El logaritmo de 1 es 0, cualquiera que sea la base
- El logaritmo de un producto es igual a la suma de los logaritmos de los factores
- El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador
- El logaritmo de una potencia es igual al exponente por el logaritmo de la base de la potencia
- El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice
- Cambio de base: El logaritmo en base a de un número se puede obtener a partir de logaritmos en otra base
EJEMPLOS:
a) log2 4 = log2 22 = 2 log2 2
= 2
DEFINICIÓN DE LOGARITMOS
LOGARITMO
Es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponencial de la base del logaritmo.

EJEMPLO:
PARTES DE LOGARITMO

¿COMO REPRESENTAR UN LOGARITMO?
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10.
la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponencial de la base del logaritmo.
EJEMPLO:
PARTES DE LOGARITMO
¿COMO REPRESENTAR UN LOGARITMO?
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
| Logaritmo | ||
|---|---|---|
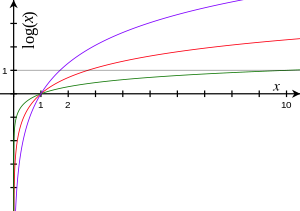 Gráfica de Logaritmo | ||
| Definición |   | |
| Tipo | Función real | |
| Descubridor(es) | John Napier (1614) | |
| Dominio | 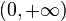 | |
| Codominio |  | |
| Imagen |  | |
| Propiedades | Biyectiva Cóncava Estrictamente creciente Trascendente | |
Suscribirse a:
Comentarios (Atom)